51 树的定义与操作
树的定义与操作
-
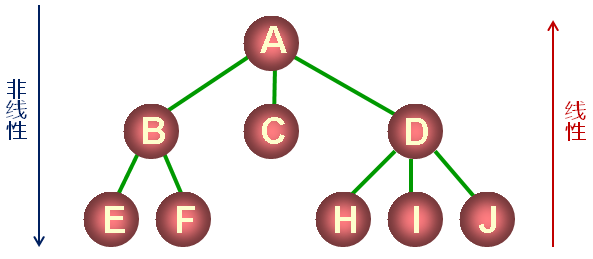
树是一种非线性的数据结构
-
树是由n(n≥0)个节点组成的有限集合
- 如果n=0,则称空树;
- 如果n>0,则:
- 有一个特定的称之为根(root)的结点
- 根结点只有直接后继,没有直接前驱
- 除根以外的其它节点划分为m(m≥0)个互不相交的有限集合T0,T1,...,Tm-1,每个集合又是一棵树,并且称之为根的子树(sub tree)
-
树的示例
-
树中度的概念
- 树的结点包含一个数据及若干指向子树的分支
- 结点拥有的子树数目称为结点的度
- 度为0的节点称为叶结点
- 度不为0的节点称为分支结点
- 树的度定义为所有结点中度的最大值
-
树的度示例:度为3的树
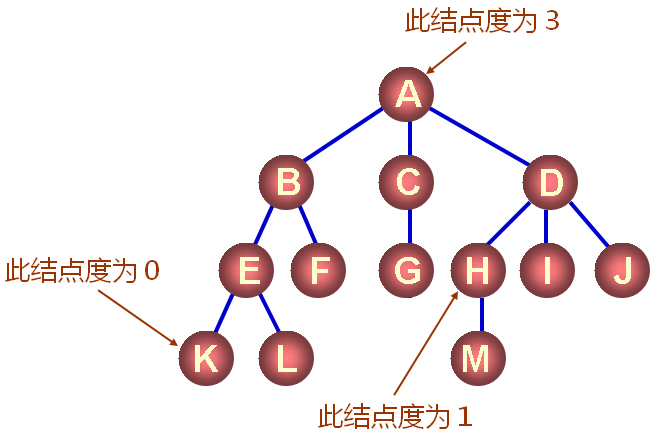
-
树中的前驱和后继
- 结点的直接后继称为该结点的孩子
- 相应的,该结点称为孩子的双亲
- 结点的孩子的孩子的......称为该结点的子孙
- 相应的,该结点称为子孙的祖先
- 同一个双亲的孩子之间互称兄弟
- 结点的直接后继称为该结点的孩子
-
树的前驱和后继示例
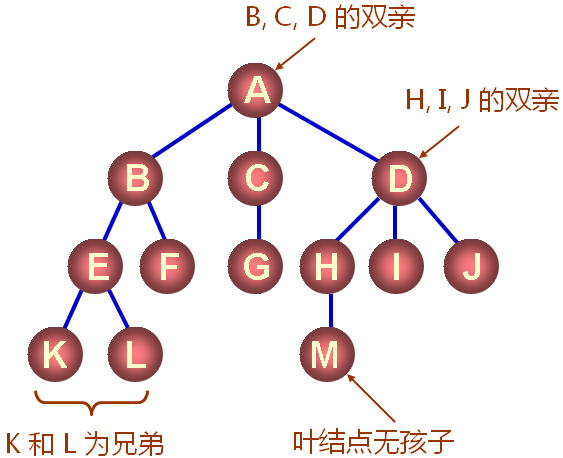
-
树中结点的层次
- 根为第一层
- 根的孩子为第二层
- ... ...
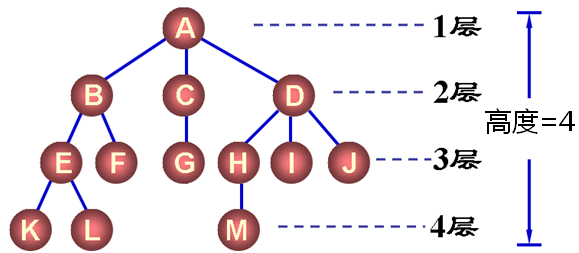
树中的结点的最大层次称为树的深度或高度
-
树的有序性 如果树中结点的各子树从左向右是有次序的,子树间不能互换位置,则称该树为有序树,否则为无序树。

-
森林的概念
-
森林是由n(n≥0)棵互不相交的树组成的集合
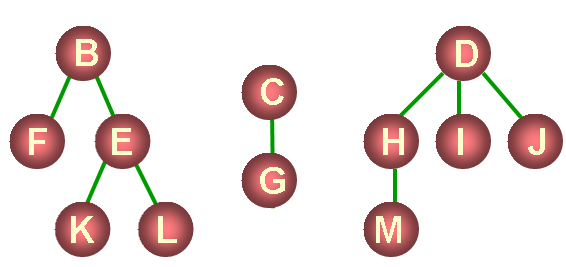
由3棵树组成的森林
-
-
树的一些常用操作
- 将元素插入树中
- 将元素从树中删除
- 获取树的结点数
- 获取树的高度
- 获取树的度
- 清空树中的元素
- ......
-
树在程序中表现为一种特殊的数据类型
template <typename T>
class Tree:public Object {
protected:
TreeNode<T>* m_root;
public:
Tree(){m_root=nullptr;}
virtual bool insert(TreeNode<T> *node)=0;
virtual bool insert(const T &value,TreeNode<T> *parent)= 0;
virtual SharedPointer<Tree<T>>remove(const T &value)=0;
virtual SharedPointer<Tree<T>>remove(TreeNode<T> *node) = 0;
virtual TreeNode<T>* find(const T &value)const = 0;
virtual TreeNode<T>* find(TreeNode<T> *node)const=0;
virtual TreeNode<T>* root()const = 0;
virtual int degree()const = 0;
virtual int count()const=0;
virtual int height()const=0;
virtual void clear() = 0;
}
- 树中的结点也表现为一种特殊的数据类型
template<typename T>
class TreeNode:public Object {
public:
T value;
TreeNode<T>* parent = nullptr;
virtual ~TreeNode()=0;
}
-
树与结点的关系
编程实验
-
树与结点抽象类的创建
#include "Object.h"
#include "TreeNode.h"
namespace Kylin {
template<typename T>
class Tree : public Object {
public:
virtual bool insert(TreeNode<T> *node) = 0;
virtual TreeNode<T>* find(const T &value)const=0;
virtual TreeNode<T>* find(TreeNode<T> *node)const=0;
virtual TreeNode<T>* root()const = 0;
virtual int degree()const =0;
virtual int count()const=0;
virtual int height()const=0;
virtual void clear()=0;
protected:
TreeNode<T> *m_root = nullptr;
};
}
小结
- 树是一种非线性的数据结构
- 结点拥有唯一前驱(父结点)和若干后继(子结点)
- 树的结点包含一个数据及若干指其它节点的指针
- 树与结点在程序中表现为特殊的数据类型
52 树的存储结构与实现
树的存储结构与实现(一)
-
课程目标
-
完成树和结点的存储结构设计
-
-
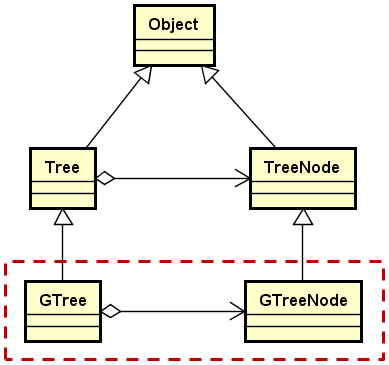
设计要点
- GTree为通用树结构,每个结点可以存在多个后继点
- GTreeNode能够包含任意多指向后继结点的指针
- 实现树结构的所有操作(增,删,查,等)
-
GTreeNode的设计与实现
template<typename T>
class GTreeNode:public TreeNode<T> {
public:
LinkList<GTreeNode<T>*> child;
} -
GTree的设计与实现
template<typename T>
class GTree:public Tree<T> {
//implementation
} -
GTree(通用树结构)的实现架构
编程实验
-
通用树结构的创建
template<typename T>
class GeneralTree : public Tree<T> {
public:
GeneralTreeNode<T>* root() const;
bool insert(GeneralTreeNode<T> *node);
bool insert(const T &value,GeneralTreeNode<T> *parent);
SharedPointer<GeneralTreeNode<T>> remove(const T &value);
SharedPointer<GeneralTreeNode<T>> remove(const GeneralTreeNode<T> *node);
// ...
};
树的存储结构与实现(二)
-
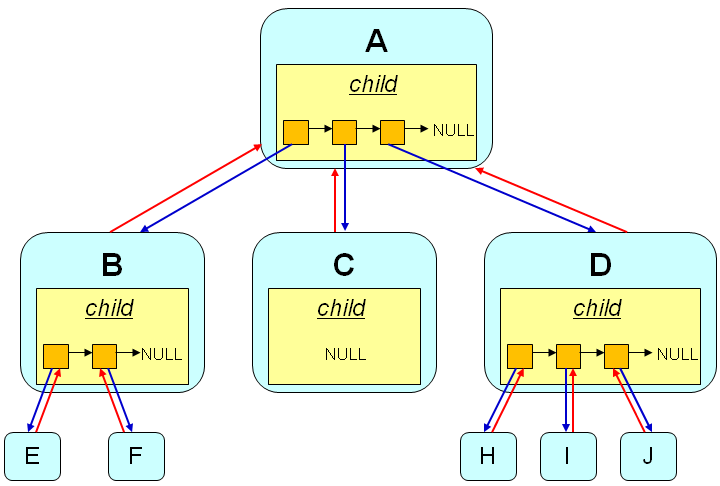
问题 每个树结点中为什么包含指向前驱结点的指针?
-
根结点->叶结点:非线性数据结构
-
叶结点->根结点:线性数据结构(链表)
思考:如何实现GeneralTree(通用树结构)的结点查找操作?